福岡の理科実験塾：エジソン少年理数工房
エジソン少年理数工房・責任者小松のひと言日記です。
円周率の世界
今は「円周率 の世界」にはまっています。
π＝3.14 は知らない方が少ないことと思われます、
が、どのようにしてこの数値を出すのか、
実際にやって見る機会は少ないのではないでしょうか。
12月前半は「浮力の世界」に続けて「円周率」の世界。
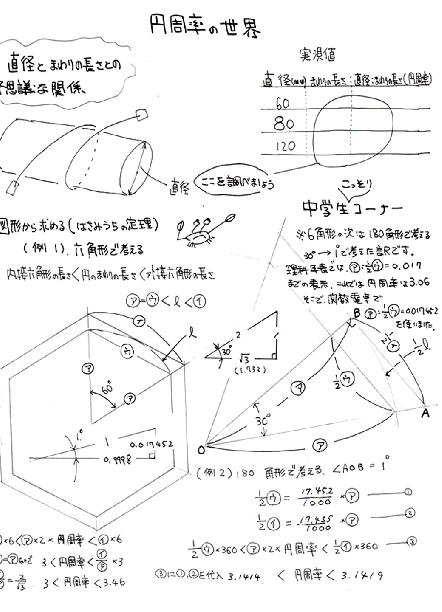
「実測」で 円周÷直径＝一定 に続けてその「一定値」を
多角形による 挟み撃ち ではじき出しすのですが
6角形を使って 内接6角形＜円周＜外接6角形
之より 3＜円周率＜3.46 ここまでは順調。
さらに多角形を使おうとしてストップ
なぜなら理科年表 表示は1度が最小。
そこで180角形で考えたのですがｓｉｎ1度＝0.017 の表示
これを使うと円周率は3.06。 やむを得ず関数電卓を使い
ｓｉｎ1度＝.017452、ｔａｎ1度＝.017455を使って
3.1414＜π＜3.1419 を出すことができました。
昔の人は一体どのようにして 5桁の三角比の値を
出したのでしょうか。不思議です。
教室便り244号もあと一歩です。
π＝3.14 は知らない方が少ないことと思われます、
が、どのようにしてこの数値を出すのか、
実際にやって見る機会は少ないのではないでしょうか。
12月前半は「浮力の世界」に続けて「円周率」の世界。
「実測」で 円周÷直径＝一定 に続けてその「一定値」を
多角形による 挟み撃ち ではじき出しすのですが
6角形を使って 内接6角形＜円周＜外接6角形
之より 3＜円周率＜3.46 ここまでは順調。
さらに多角形を使おうとしてストップ
なぜなら理科年表 表示は1度が最小。
そこで180角形で考えたのですがｓｉｎ1度＝0.017 の表示
これを使うと円周率は3.06。 やむを得ず関数電卓を使い
ｓｉｎ1度＝.017452、ｔａｎ1度＝.017455を使って
3.1414＜π＜3.1419 を出すことができました。
昔の人は一体どのようにして 5桁の三角比の値を
出したのでしょうか。不思議です。
教室便り244号もあと一歩です。
作成日時2019/11/27 16:13:15