福岡の理科実験塾:エジソン少年理数工房



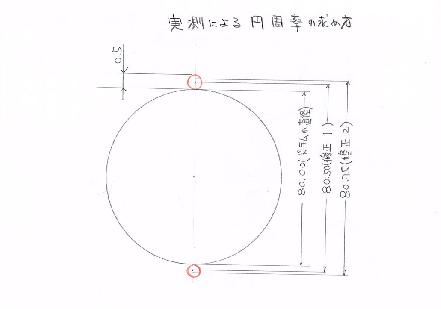
実測による円周率の求め方
誰もが抱く「円周率」を実測によって求めてみましょう。材料は直径が80ミリピッタリの筒と断面の直径が0.5ミリの銅線。道具はメジャーだけ。
〈工夫 1〉計測誤差を少なくするため銅線を筒に添って4回巻き、刻印 代わりに塗りつけるマジックインク幅の一回あたりの誤差を 4分の一にしました。
〈工夫 2〉メジャーは端のつめの部分は使わず100ミリのラインから使用 しました。(大工がよく使う方法です)
〈計測値〉 スタートラインから終了ラインまで1013ミリ。
〈第一回計算〉 1013÷4=253.25(一巻きあたりの長さ)
253・25÷80=3・1656
〈第一回 修正〉図のように銅線は直径0.5ミリの太さを持ちます。つまり
今回計ったのは直径80ミリではなく銅線の太さを含む直 系を測ったのです。
では計った直径は何ミリだったのでしょう。物理の世界では
距離は中心から中心までとされていますから0.5ミリの半分の 0.25ミリを80ミリの両端に加えた長さ、つまり80.5ミリ
〈第二回 計算〉253.25÷80.5=3.1459 となりました。
〈第二回 修正〉金属は延びやすくはあっても縮みにくい性質があります
筒に巻きつけられた銅線が伸びもしないし縮みもしない
断面上の位置はどこなのか?
ここからは門外漢なのですが仮説として中心部からさらに
外に向かって半分の位置つまり銅線の中心から0.125ミリ
外側の点で計算して見ました。
〈第二回 計算〉253.25÷80.75=3.136 となり、がっかり
〈逆算 したら 〉 253025÷3.14159=80.612と判明しました。
*直径が80ミリ以外でもやる必要がありますが、やり方としてなにかの参考になればと思います。
〈工夫 1〉計測誤差を少なくするため銅線を筒に添って4回巻き、刻印 代わりに塗りつけるマジックインク幅の一回あたりの誤差を 4分の一にしました。
〈工夫 2〉メジャーは端のつめの部分は使わず100ミリのラインから使用 しました。(大工がよく使う方法です)
〈計測値〉 スタートラインから終了ラインまで1013ミリ。
〈第一回計算〉 1013÷4=253.25(一巻きあたりの長さ)
253・25÷80=3・1656
〈第一回 修正〉図のように銅線は直径0.5ミリの太さを持ちます。つまり
今回計ったのは直径80ミリではなく銅線の太さを含む直 系を測ったのです。
では計った直径は何ミリだったのでしょう。物理の世界では
距離は中心から中心までとされていますから0.5ミリの半分の 0.25ミリを80ミリの両端に加えた長さ、つまり80.5ミリ
〈第二回 計算〉253.25÷80.5=3.1459 となりました。
〈第二回 修正〉金属は延びやすくはあっても縮みにくい性質があります
筒に巻きつけられた銅線が伸びもしないし縮みもしない
断面上の位置はどこなのか?
ここからは門外漢なのですが仮説として中心部からさらに
外に向かって半分の位置つまり銅線の中心から0.125ミリ
外側の点で計算して見ました。
〈第二回 計算〉253.25÷80.75=3.136 となり、がっかり
〈逆算 したら 〉 253025÷3.14159=80.612と判明しました。
*直径が80ミリ以外でもやる必要がありますが、やり方としてなにかの参考になればと思います。
作成日時2012/05/23 18:41:32